Top Important Probability Interview Questions & Answers for Data Scientists [ Mathematical Questions]

This article presents a comprehensive collection of probability interview questions and their solutions tailored for data scientists. Covering a diverse range of scenarios from coin toss games to random card selections, each question is dissected with detailed explanations and multiple solution methods, providing insights into fundamental probability concepts. 

Through a combination of theoretical reasoning, combinatorial analysis, and application of Bayes’ theorem, readers are guided through solving intricate probability problems commonly encountered in data science interviews. 

Whether preparing for interviews or seeking to deepen understanding of probability theory, this article serves as a valuable resource for data scientists navigating the intricacies of probability.

---

---

1. You and your friend are playing a game with a fair coin. The two of you will continue to toss the coin until the sequence HH or TH shows up. If HH shows up first, you win, and if TH shows up first your friend wins. What is the probability of you winning the game?

Answer:

If T is ever flipped, you cannot then reach HH before your friend reaches TH. Therefore, the probability of you winning this is to flip HH initially. Therefore the sample space will be {HH, HT, TH, TT} and the probability of you winning will be (1/4) and your friend (3/4)

---

2. If you roll a dice three times, what is the probability of getting two consecutive threes?

There are different ways to answer this question:

1. If we roll a dice three times we can get two consecutive 3’s in three ways:

2. The first two rolls are 3s and the third is any other number with a probability of 1/6 * 1/6 * 5/6.

3. The first one is not three while the other two rolls are 3s with a probability of 5/6 * 1/6 * 1/6

4. The last one is that the three rolls are 3s with probability 1/6 ^ 3

So the final result is 2 * (5/6 * (1/6)²) + (1/6)*3 = 11/216

By Inclusion-Exclusion Principle:

Probability of at least two consecutive threes = Probability of two consecutive threes in first two rolls + Probability of two consecutive threes in last two rolls — Probability of three consecutive threes

= 2 * Probability of two consecutive threes in first two rolls — Probability of three consecutive threes = 2 * (1/6) * (1/6) — (1/6) * (1/6) * (1/6) = 11/216

It can be seen also in this:

The sample space is made of (x, y, z) tuples where each letter can take a value from 1 to 6, therefore the sample space has 6x6x6=216 values, and the number of outcomes that are considered two consecutive threes is (3,3, X) or (X, 3, 3), the number of possible outcomes is therefore 6 for the first scenario (3,3,1) till (3,3,6) and 6 for the other scenario (1,3,3) till (6,3,3) and subtract the duplicate (3,3,3) which appears in both, and this leaves us with a probability of 11/216.

---

3. Suppose you have ten fair dice. If you randomly throw them simultaneously, what is the probability that the sum of all of the top faces is divisible by six?

Answer: 1/6

Explanation: With 10 dice, the possible sums divisible by 6 are 12, 18, 24, 30, 36, 42, 48, 54, and 60. You don’t need to calculate the probability of getting each of these numbers as the final sums from 10 dice because no matter what the sum of the first 9 numbers is, you can still choose a number between 1 to 6 on the last die and add to that previous sum to make the final sum divisible by 6. Therefore, we only care about the last die. And the probability of getting that number on the last die is 1/6. So the answer is 1/6.

---

4: If you have three draws from a uniformly distributed random variable between 0 and 2, what is the probability that the median of three numbers is greater than 1.5?

The right answer is 5/32 or 0.156. There are different methods to solve it:

Method 1

To get a median greater than 1.5 at least two of the three numbers must be greater than 1.5. The probability of one number being greater than 1.5 in this distribution is 0.25. Then, using the binomial distribution with three trials and a success probability of 0.25 we compute the probability of 2 or more successes to get the probability of the median is more than 1.5, which would be about 15.6%.

Method 2

A median greater than 1.5 will occur when o all three uniformly distributed random numbers are greater than 1.5 or 1 uniform distributed random number between 0 and 1.5 and the other two are greater than 1.5.

So, the probability of the above event is = {(2–1.5) / 2}³ + (3 choose 1)(1.5/2)(0.5/2)² = 10/64 = 5/32

Method3:

Using the Monte Carlo method as shown in the figure below:

---

5: Assume you have a deck of 100 cards with values ranging from 1 to 100 and you draw two cards randomly without replacement, what is the probability that the number of one of them is double the other?

There are a total of (100 C 2) = 4950 ways to choose two cards at random from the 100 cards and there are only 50 pairs of these 4950 ways that you will get one number and it’s double. Therefore the probability that the number of one of them is double the other is 50/4950.

---

6. If there are 30 people in a room, what is the probability that everyone has different birthdays?

The sample space is 365³⁰ and the number of events is 365p30 because we need to choose persons without replacement to get everyone to have a unique birthday, therefore, the Prob = 356p30 / 365³⁰ = 0.2936.

Here are some interesting facts:

1. With just 23 people there is over 50% chance of a birthday match and with 57 people the match probability exceeds 99%. One intuition to think of why with such a low number of people the probability of a match is so high. It’s because for a match we require a pair of people and 23 choose 2 is 23*11 = 253 which is a relatively big number and ya 50% sounds like a decent probability of a match for this case.

2. Another interesting fact is if the assumption of equal probability of the birthday of a person on any day out of 365 is violated and there is a non-equal probability of the birthday of a person among days of the year then, it is even more likely to have a birthday match.

---

8. Assume two coins, one fair and the other is unfair. You pick one at random, flip it five times, and observe that it comes up as tails all five times. What is the probability that you are flipping the unfair coin?

Answer:

Let’s use Baye’s theorem let U denote the case where you are flipping the unfair coin and F denote the case where you are flipping the fair coin. Since the coin is chosen randomly, we know that P(U)=P(F)=0.5. Let 5T denote the event of flipping 5 tails in a row.

Then, we are interested in solving for P(U|5T) (the probability that you are flipping the unfair coin given that you obtained 5 tails). Since the unfair coin always results in tails, therefore P(5T|U) = 1 and also P(5T|F) =1/²⁵ = 1/32 by the definition of a fair coin.

Lets apply Bayes theorem where P(U|5T) = P(5T|U) * P(U) / P(5T|U)* P(U) + P(5T|F)* P(F) = 0.5 / 0.5 +0.5* 1/32 = 0.97

Therefore the probability that you picked the unfair coin is 97%

---

9. Assume you take a stick of length 1 and break it uniformly at random into three parts. What is the probability that the three pieces can be used to form a triangle?

Answer: 

Let’s say, x and y are the lengths of the two parts, so the length of the third part will be 1-x-y

As per the triangle inequality theorem, the sum of two sides should always be greater than the third side. Therefore, no two lengths can be more than 1/2. x<1/2 y<1/2

Based on the triangle inequality theorem: x+y > 1-a-b x+y > 1/2

From the diagram below, there is only one triangle that matches all the above conditions out of 4 triangles. Therefore, the probability will be 1/4

---

10. Say you draw a circle and choose two chords at random. What is the probability that those chords will intersect?

Answer: 

For making 2 chords, 4 points are necessary and from 4 points there are 3 different combinations of pairs of chords that can be made. From the 3 combinations, there is only one combination in which the two chords intersect hence answer is 1/3. 

Let’s assume that P1, P2, P3, and P4 are four points then 3 different combinations are possible for pairs of chords: (P1 P2) (P3 P4) or (P1 P3) (P4 P2) or (P1 P4) (P2 P3) there the 3rd one will only intersect.

---

11. If there’s a 15% probability that you might see at least one airplane in a five-minute interval, what is the probability that you might see at least one airplane in a period of half an hour?

Answer:

Probability of at least one plane in 5 mins interval=0.15 Probability of no plane in 5 mins interval=0.85 Probability of seeing at least one plane in 30 minutes = 1 — Probability of not seeing any plane in 30 minutes =1-(0.85)⁶ = 0.6228.

---

12. Say you are given an unfair coin, with an unknown bias towards heads or tails. How can you generate fair odds using this coin?

Answer:

---

13. According to hospital records, 75% of patients suffering from a disease die from that disease. Find out the probability that 4 out of the 6 randomly selected patients survive.

Answer: 

This has to be a binomial since there are only 2 outcomes — death or life.

Here n =6, and x=4.

p=0.25 (probability if life) q = 0.75(probability of death)

Using probability mass function equation:

P(X) = nCx *p q(n-x)

Then:

P(4) = 6C4* (0.25)4(0.75)*2 = 0.032

---

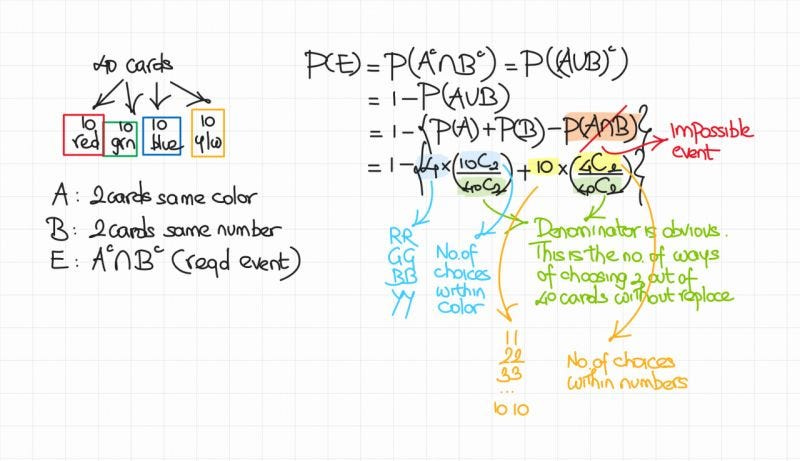
15. You have 40 cards in four colors, 10 reds, 10 greens, 10 blues, and ten yellows. Each color has a number from 1 to 10. When you pick two cards without replacement, what is the probability that the two cards are not in the same color and not in the same number?

Answer:

Since it doesn’t matter how you choose the first card, so, choose one card at random. Now, all we have to care about is the restriction on the second card. It can’t be the same number (i.e. 3 cards from the other colors can’t be chosen in favorable cases) and also can’t be the same color (i.e. 9 cards from the same color can’t be chosen keep in mind we have already picked one).

So, the number of favorable choices for the 2nd card is (39–12)/39 = 27/39 = 9/13

---

Are you looking to start a career in data science and AI and do not know how? I offer data science mentoring sessions and long-term career mentoring:

• Mentoring sessions: https://lnkd.in/dXeg3KPW

• Long-term mentoring: https://lnkd.in/dtdUYBrM